Trending Now
How To
Valorant Error Code 57 – Fixed it
Are you constantly facing the Valorant error code 57, which prevents you from playing your games? We are here to help you fix it!
Valorant,...
Discord
Business
Login Process
Minecraft
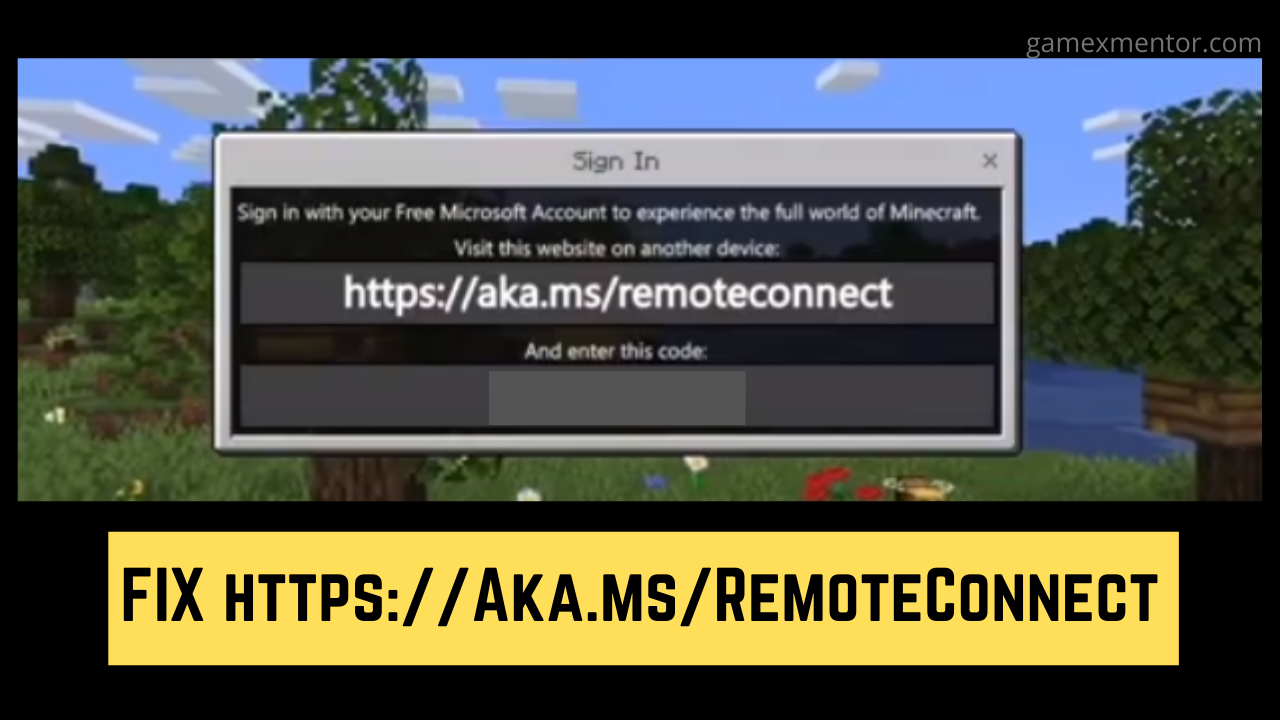
Https://Aka.Ms/RemoteConnect- Minecraft Remote Connect on Xbox, Playstation And Nintendo
Are you experiencing difficulty while attempting to sign in to your Microsoft account, The https://aka.ms/remoteconnect issue is normal for a great deal of Minecraft...
Essential Factors to Consider When Choosing a Minecraft Server
Minecraft is one of the world’s most popular online games. Sadly though, many online servers are plagued by griefers and trolls. If you aren’t...